Except for String Theory, most of the references above have achieved great success by describing space itself has having discrete or “quantum” structure to it. This means that space is not empty, but made of a lattice of energy that literally makes up the “spacetime fabric.” If we come to understand this fabric, and the fundamental structure of space (which makes up 99.99999% of the universe), than we have the basic tools to adjust not only dynamics of electromagnetism, but gravity as well.
After studying the equations for quantum gravitation by Lee Smolin and team, and considering the work of Buckminster Fuller, it became very clear that the spacetime fabric would contain a regular platonic geometry. Although the postulations for quantum foam and the spin networks illustrated by Smolin are rough and chaotic, it makes far more sense to consider that the natural conservation of energy is at work as much at the smallest scales as it is on the largest.
It also became clear that some signatures of the most basic arrangements of the spacetime fabric would be found through all cultures, in all forms of plant and animal life, and be revealed in the heart of world religions. I postulated and tested these basic assumptions as a teenager, and have found confirmations continuously since that time. Assurance as to the fundamental geometry only grew stronger as I discovered Nassim Haramein’s work, which mapped the three-dimensional stacking process of the structure in equilibrium out to a 64 tetrahedral matrix.
For the purposes of my study, I found it more interesting to look at the basic permutations of geometry. My own study, and that of Buckminster Fuller was most informing in this process, and I found that each simple geometric permutation describes one of the fundamental forces perfectly…
First, let’s look at the fundamental structure of the fabric of space-time. If we consider the most basic possible information structures at the Planck scale, a Planck length line is the most fundamental representation of distance (1D), and a triangle made from three of these lines would form the most fundamental structure of area (2D). Moving up to the next most fundamental dimensional structure, we obtain a Planck scale tetrahedron (3D). From here, we obtain a component that can form a lattice structure that has both planar surfaces and extruded depth, both of which are measured in both space and time.
Each unit of Planck space is also a unit of time, since the distance itself cannot exist in measurement without some measure of time. In this way, we could say that the dimension of time (4D) is embedded, entangled, or folded into each of these three spacial dimensions.
It is also important to look at our most fundamental building block, the triangle, more closely. Through the laws of thermodynamics, we know that energy and matter is always trying to reach the most balanced state. Heat will continue to flow into cool space until the temperature is equalized. Spheres thrown into a box will continue to compact with each other until they reach the maximum state of spacial density, which at the same time is the lowest state of potential energy (or mobility).
When discussing a lattice of energy, each node (or intersection point) will try to reach the position in which it has the most equal balance with all surrounding points. This is simply another way of describing why the equilateral triangle, and its 3D projection, the tetrahedron, is the most fundamental and equalized structural form for space-time.
If energy, and thus the fabric of spacetime, is always trying to maintain an equilibrium state, then any condition outside of that state of equilibrium will produce force (an influence that may cause a body to accelerate, or produce Gravity).
From here, we may begin to review each of the permutations of this fundamental lattice that would produce different levels of force, and thus produce Gravity.
“Any polygon with more than three sides is unstable. Only the triangle is inherently stable. Any polyhedron bounded by polygonal faces with more than three sides is unstable. Only polyhedra bounded by triangular faces are inherently stable.” -Buckminster Fuller
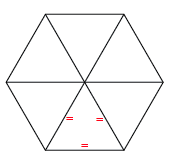
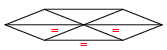
In any equilateral triangular lattice surface, if you remove one of the triangles, the entire surface will bend in order to keep the equilibrium intact.
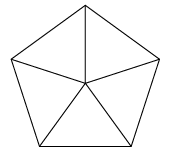
It is this principle that holds the secret to Buckminster Fuller’s work, and allows the curvature of structures to be modulated by adjusting the distance between the areas where this triangle has been removed. In these places, the Hexagonal “plate” has now “warped” into a Pentagonal plate, and this change in geometry in a single position allows curvature for the entire surface. At maximum Pentagonal curvature, these Pentagonal plates are directly adjacent to each other, which will tighten into an Icosahedron.
Because of this simple modulation to the equilateral surface, curvature has been established, and a basic “unit of Gravity” in the structure of space-time has been identified.
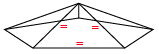
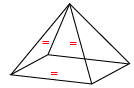
With enough energy, after the Pentagonal curvature reaches its maximum state (Icosahedral arc), the structure of spacetime can be forced to curve even further, and another triangle in the equilibrium “pressed” off of the surface lattice. This will tighten the four remaining triangles of the surface into a pyramid shape. This state of compression and change in the lattice has a rippling effect, as each of the vector planes curve to adjust to the insertion of a “square” unit.
This effect is intimately involved with the series of energetic alterations that produce physical matter from energy within the fabric of space-time, but we will not go into depth here on that process. However, we must recognize that at this level of curvature there is no longer a gradual spherical curve on spacetime, just an abrupt compression point of energy. This may be the key to the vector equilibrium form, and may form the entry point into a black hole or singularity.
“There are only three possible cases of fundamental omnisymmetrical, omnitriangulated, least-effort structural systems in nature: the tetrahedron with three triangles at each vertex, the octahedron with four triangles at each vertex, and the icosahedron with five triangles at each vertex. If there are six equilateral triangles around a vertex we cannot define a three-dimensional structural system, only a ‘plane.'” – Buckminster Fuller
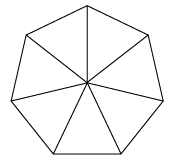
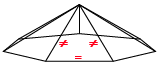
Any time a triangle is “removed” from one plane of equilibrium, or from a curvature, it cannot simply be “added” to another Hexagonal lattice. If you attempt to insert an additional equilateral triangle into a Hexagon, you will find that there is no amount of angular adjustment you can make to allow it to fit.
Therefore one of two things must happen:
(1) The equilateral triangles in the set “warp” and become acute triangles in order to accomodate the new trianglular energy field, which would take a vast amount of energy since these structures want to remain in equilibrium and this would change the balance of the entire fabric.
(2) The equilateral triangle connects to one of the triangles in the set, and the new triangle now “rotates” into a position connecting with one of the other vector equilibrium planes. The initial act of this rotation into position would cause the torsion forces in the fabric of space-time described by Nassim Haramein and others.
Being that the latter option would require far less energy, it is certainly the more likely scenario, and generates other notable effects. First of all, the rotation of a new triangle, or more specifically a single “point” of force (since it is actually only one node or intersection on the structure that needs to be removed) from one surface into any other plane of the Hexagonal vector equilibrium would produce a chain reaction, in which that Hexagonal plane would then transfer one of its own “points” to the next adjacent plane, and so on.
This would look like a ripple effect, in which a point of energy in the fabric of space-time would go spinning through the lattice until it found a stable position to rest, or “nest.” Energy transference in this form is limited to the speed at which each Planck unit of distance in the structure can exchange with the next, which would be the fundamental measure of the speed of energy exchange through the fabric of space-time. This speed of course, is the “speed of light,” which in turn provides the fundamental unit of “time” to the vector equilibrium of space, as it provides the relative measure of separation between any point in the lattice with any other point.
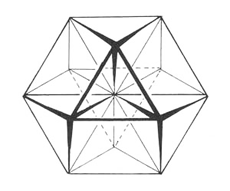
Now if we consider each one of the individual points in this lattice, we see that while in a vector equilibrium state, there are 18 radials extending to other points in the matrix along spacial dimensions. The points are intersections of energy, bridging dimensions. Each point in the lattice may fluxuate as energy passes through it, as vibration travels through these dimensional radials.
The state of a point or intersection at any given moment is determined by the combination of vibrations moving through it. Each structural intersection is not only a position, but also resonates at a specific frequency. In this way, even the planck scale structure of space-time is not a static and rigid system, but is flexible and acts in accordance with the properties of waveforms and fluid dynamics.
Energy will always attempt to reach an equilibrium state, so the dynamics at this scale are in a constant flux, working to return balance to the fundamental fabric. Each change that precipitates this “returning” ripples through the fabric, and can be seen from microcosmic to macrocosmic scales.
